How AI Works: A Layman’s Guide
This article provides a detailed, accessible explanation of how Artificial Intelligence (AI) works, focusing on the role of mathematics (linear algebra, probability, and optimization), the differences between Small Language Models (SLMs), Large Language Models (LLMs), and Context-Specific LLMs, and a high-level “mental picture” of AI system operations. It’s designed for system design interviews, beginners, and engineers seeking a deeper understanding of AI fundamentals.
What is AI?
Artificial Intelligence (AI) refers to systems or machines that mimic human intelligence to perform tasks such as problem-solving, decision-making, or pattern recognition. At its core, AI is about learning from data to make predictions, classifications, or generate outputs without being explicitly programmed for every scenario.
AI systems rely on data, algorithms, and computing power to:
- Learn patterns (e.g., recognizing images or language).
- Make decisions (e.g., recommending movies).
- Generate content (e.g., text, images).
The Role of Mathematics in AI
Mathematics is the backbone of AI, enabling machines to process data, learn patterns, and optimize decisions. The three key mathematical pillars are linear algebra, probability, and optimization.
1. Linear Algebra: The Language of Data
Linear algebra deals with vectors, matrices, and their operations, which are essential for representing and manipulating data in AI.
Why It Matters:
- Data (e.g., images, text) is often represented as vectors (lists of numbers) or matrices (grids of numbers).
- Neural networks perform computations using matrix operations (e.g., dot products).
- For example, an image might be a matrix of pixel values, and a neural network layer transforms it via matrix multiplication.
Key Concepts:
- Vectors: Represent data points (e.g., a word’s embedding in a language model).
- Matrices: Represent transformations or weights in a neural network.
- Tensors: Higher-dimensional arrays used in deep learning (e.g., 3D video data).
- Matrix Operations: Multiplication, transposition, inversion.
Real-World Example: In image recognition, linear algebra transforms a photo (pixels) through layers of a neural network to identify objects.
2. Probability: Handling Uncertainty
Probability provides the framework for dealing with uncertainty, which is central to AI’s ability to make predictions.
Why It Matters:
- Models output probabilities (e.g., “80% chance this is a cat”).
- Helps assign confidence scores and handle noisy data.
- In language models, probabilities guide the choice of the next word.
Key Concepts:
- Probability Distributions: Likelihood models.
- Bayes’ Theorem: Updating beliefs with evidence.
- Softmax Function: Converts raw scores into probabilities.
- Markov Chains: Sequence modeling.
Real-World Example: A spam filter calculates the probability that an email is spam based on word frequencies.
3. Optimization: Learning from Data
Optimization is how AI models improve by adjusting parameters to minimize errors.
Why It Matters:
- Models learn by reducing errors in predictions.
- Optimization fine-tunes millions (or billions) of weights in a network.
Key Concepts:
- Loss Function: Measures error (e.g., mean squared error).
- Gradient Descent: Iteratively adjusts weights.
- Backpropagation: Efficient gradient calculation.
- Learning Rate: Step size in optimization.
Real-World Example: Training a digit-recognition model to correctly identify handwritten numbers.
From Mathematics to Omniscience: Why AI Feels Like It Knows Everything
To many, interacting with an AI feels like speaking to an all-knowing oracle. It can answer questions, generate stories, write code, and even solve math problems. But behind the scenes, it’s not magic—it’s mathematics.
Why It Feels Omniscient
- AI systems are trained on massive datasets (billions of text examples, images, code, etc.).
- The model learns statistical patterns between inputs and outputs.
- When you ask a question, it retrieves and recombines patterns, giving the illusion of understanding.
The result: AI appears to “know everything” because it has compressed knowledge of the training data into a mathematical structure.
The Math Beneath the Illusion
- Linear Algebra: Every word, image pixel, or sound is represented as a vector in high-dimensional space.
- Probability: The model doesn’t “decide” what to say; it calculates the most probable next token.
- Optimization: Through training, millions or billions of parameters are adjusted to reduce prediction error.
These mechanics let AI recall patterns with astonishing accuracy—appearing “intelligent” when in fact it’s executing statistical math at scale.
Example: Predicting a Word
Suppose you type:
“The capital of France is …”
- The AI converts your text into vectors.
- It computes probabilities for the next word:
- Paris: 0.95
- London: 0.02
- Rome: 0.01
- It picks the highest probability (“Paris”).
To you, it feels like the AI knows geography. In reality, it’s leveraging probability and prior training data.
Mental Model
Think of AI like a mathematical crystal ball:
- It doesn’t see the future.
- It projects the most likely continuation of patterns it has learned.
- The “omniscience” is really pattern recognition at scale, powered by math.
Language Models: SLMs, LLMs, and Context-Specific LLMs
Language models process and generate human-like text. They vary by size and purpose.
1. Small Language Models (SLMs)
- Definition: Compact models with fewer parameters (millions to a few billion), designed for efficiency and specific tasks.
- Characteristics: Fast, low compute, on-device friendly; limited general reasoning.
- Use Cases: Autocorrect, on-device assistants, lightweight chatbots.
- Examples: DistilBERT, MobileBERT, small fine-tuned variants of transformer models.
2. Large Language Models (LLMs)
- Definition: Massive models with billions to trillions of parameters, trained on internet-scale datasets.
- Characteristics: Broad world knowledge, strong generative and reasoning capabilities; expensive to train & serve.
- Use Cases: Conversational AI, content generation, summarization, research tools.
- Examples: GPT-4, LLaMA, PaLM.
3. Context-Specific LLMs
Definition: Models (often derived from base LLMs) that are adapted and optimized for a particular domain, dataset, or task. They bridge the gap between general LLMs and SLMs by combining strong language understanding with domain relevance and efficiency.
How They Are Built:
- Fine-Tuning: Continue training a base LLM on domain-specific labeled data (e.g., clinical notes for healthcare).
- Instruction Tuning: Teach the model to follow domain-specific prompts or formats (e.g., legal contract clauses).
- Prompt Engineering / Prompt Tuning: Carefully craft prompts or learn prompt tokens to steer behavior without full retraining.
- Parameter-Efficient Methods: Techniques like LoRA (Low-Rank Adapters), Adapter modules, and prefix tuning that adapt models with fewer parameters and lower compute costs.
- Retrieval-Augmented Generation (RAG): Combine an LLM with a vector database / retriever to fetch relevant documents and provide grounded responses — especially useful when the domain knowledge is large or changing.
Characteristics:
- Domain Expertise: More accurate and reliable for industry tasks (healthcare, legal, finance).
- Smaller Footprint: Typically smaller or more efficient than full LLMs after adaptation (using LoRA, adapters, or pruning).
- Safer / More Controlled: Can be constrained to domain safe-lists, business rules, or compliance requirements.
- Update-Friendly: RAG allows updating knowledge without retraining the whole model.
Use Cases:
- Medical diagnosis support (interpreting patient records, suggesting tests).
- Legal document review (finding clauses, drafting summaries).
- Enterprise assistants (knowledge base Q&A, internal SOP guidance).
- Customer support with product-specific knowledge.
Trade-Offs:
- Pros: Higher accuracy on domain tasks, lower inference cost vs full LLMs, easier compliance controls.
- Cons: Limited generalization outside domain, requires curated domain data and evaluation, potential for domain-specific biases.
Comparison Table (Updated with Context-Specific LLMs)
| Aspect | SLMs | LLMs | Context-Specific LLMs |
|---|---|---|---|
| Parameter Count | Millions to low billions | Billions to trillions | Typically mid-size after adaptation (or base LLM + adapters) |
| Scope | Narrow, task-focused | Broad, general-purpose | Domain-specific (medical, legal, enterprise) |
| Compute Needs | Low (edge devices) | Very high (GPUs/TPUs in data centers) | Moderate (adapters/LoRA/RAG reduce cost) |
| Use Case | Autocorrect, on-device assistants | Conversational AI, content creation | Enterprise assistants, domain Q&A, compliance tasks |
| Training Data | Small, curated datasets | Massive, diverse datasets | Domain-specific corpora + base LLM pretraining |
| Performance | Fast, cheap, limited capability | Very capable, costly | High domain accuracy, cost-effective vs full LLM |
| Updating Knowledge | Retrain or small updates | Expensive retrain | RAG allows fast knowledge updates; adapters allow quick fine-tuning |
| Safety & Control | Easier to constrain | Harder to fully control | Easier to enforce domain rules and safety filters |
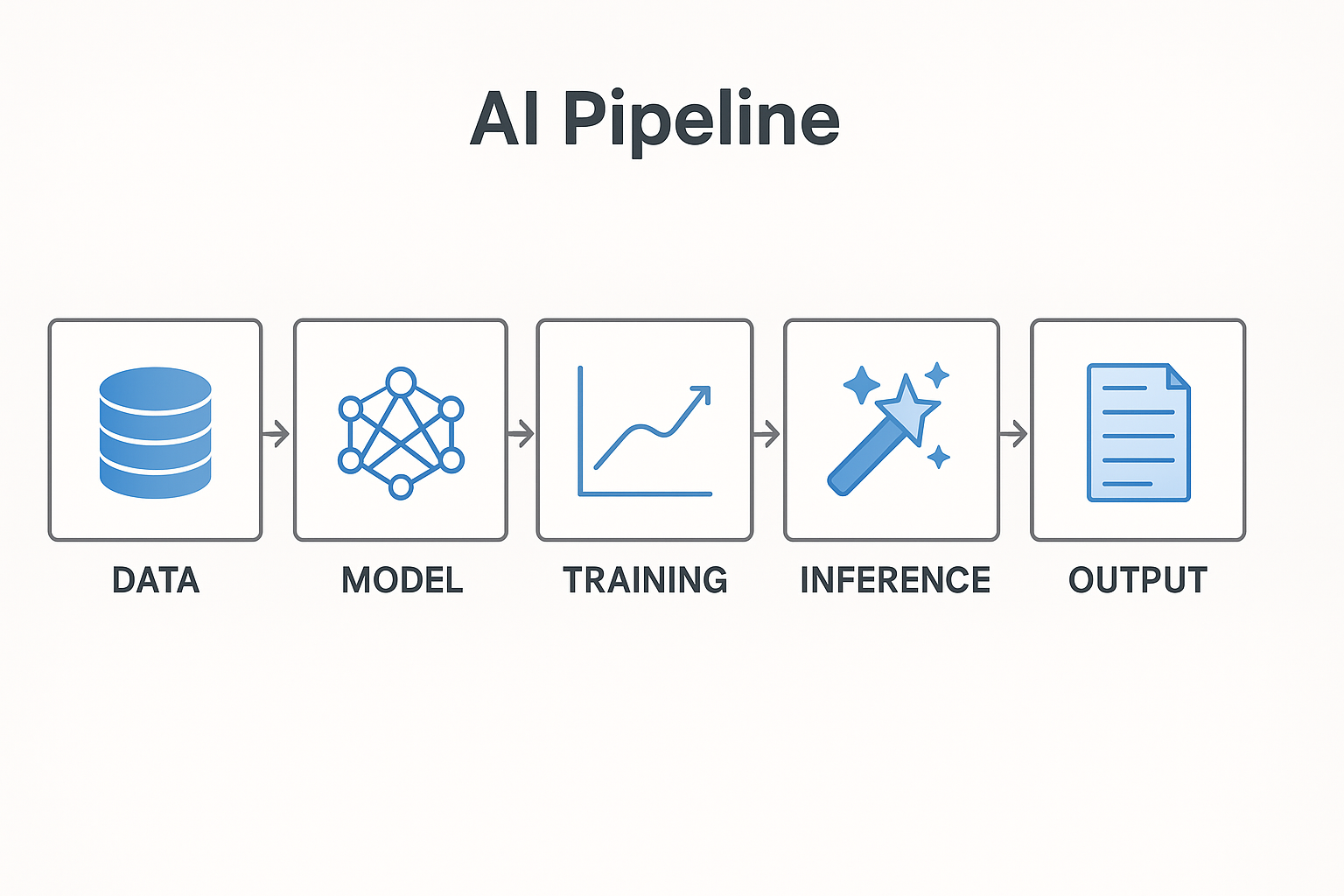
High-Level Mental Picture of How AI Systems Operate
To understand AI systems, imagine a pipeline that transforms raw data into meaningful outputs, driven by layers of computation and learning.
- Data Input → Text, images, audio, or numerical values.
- Preprocessing → Clean, tokenize, normalize, and convert to embeddings.
- Model Architecture → Neural networks (e.g., Transformers) process embeddings.
- Training Phase → Optimize weights using loss functions and gradient descent.
- Inference Phase → Apply model to new data; may call RAG retrievers for domain data.
- Output & Feedback → Model returns predictions; feedback refines future training.
Factory Analogy: Raw Materials (Data) → Assembly Line (Model) → Quality Control (Loss) → Product (Output).
FAQ: Common Beginner Questions
Q1. Is AI just math?
Yes — AI relies heavily on math (linear algebra, probability, optimization), but it also requires engineering (data pipelines, compute), domain knowledge, and user design.
Q2. Why are GPUs important for AI?
GPUs accelerate matrix math and parallel operations, dramatically reducing training time for large models.
Q3. What's the difference between SLMs, LLMs, and Context-Specific LLMs?
- SLMs: Small and efficient for simple tasks.
- LLMs: Huge, general-purpose, and powerful.
- Context-Specific LLMs: Tuned/adapted for a particular domain — they combine efficiency and domain accuracy.
Q4. What is RAG and why is it useful?
RAG (Retrieval-Augmented Generation) fetches relevant documents from a knowledge base and provides them as context to the LLM, improving factual accuracy and enabling knowledge updates without full retraining.
Q5. Will Context-Specific LLMs replace general LLMs?
No — they complement each other. General LLMs provide broad capabilities while context-specific models provide reliable, domain-focused behavior where accuracy and compliance matter.
Real-World Context
- Interview Relevance: Explain AI pipelines, differences between model types, and when to use RAG or adapters.
- Practical Use: Engineers pick model types based on latency, accuracy, cost, and compliance.
- Trends: Efficient fine-tuning (LoRA, adapters), RAG, and responsible AI practices for domain deployments.
Further Reading
- Deep Learning — Goodfellow, Bengio, Courville
- Neural Networks and Deep Learning — Michael Nielsen (free online)
- Attention is All You Need — Vaswani et al., 2017 (Transformer paper)
- Blogs: OpenAI, Hugging Face, NVIDIA — model engineering guides